Espace des fanatiques des mathématiques
Nous donnons danc cette rubrique des exercices et des problème qui intéressent les amoureux des énigmes mathématiques … On leur donnera le nom de Epsilon1, Epsilon2, etc. …C’est un espace ouvert et les contributions pour enrichir cette rubrique en proposaTrouver cnt des questions mathématiques amusantes sont les bienvenues. Ecrire à contact@epsilon.tn .

Epsilon 72
Comment distribuer entre trois personnes vingt-une bouteilles, dont sept pleines, sept vides & sept demi-pleines, en sorte que chacune ait la même quantité d’huile & de bouteilles ?

Epsilon 71

Epsilon 70

Epsilon 69
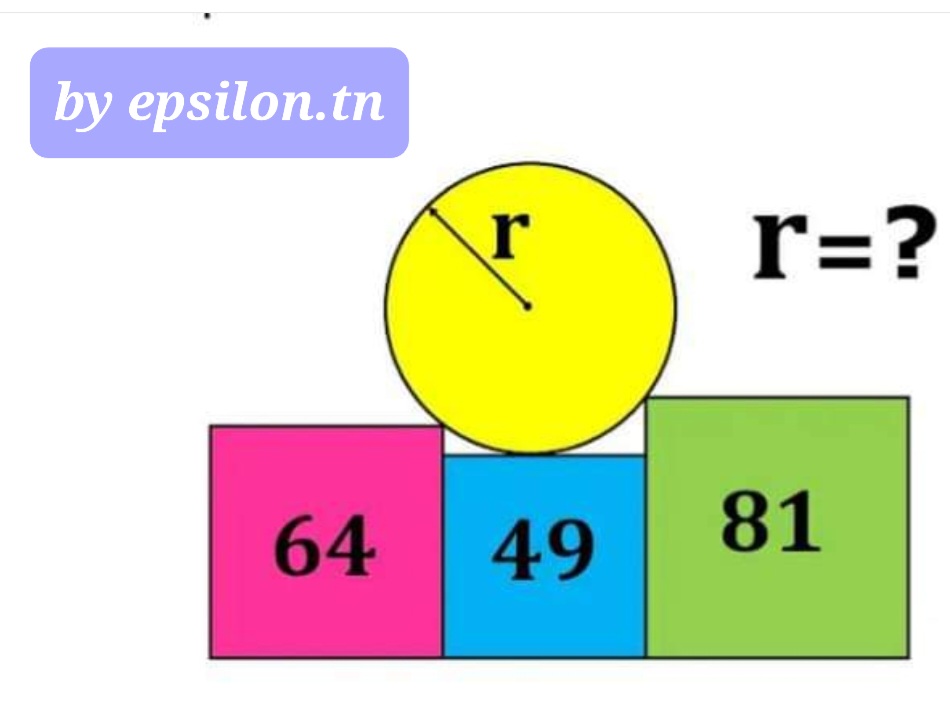
Allez … un peu de Pythagore les enfants!

Epsilon 68
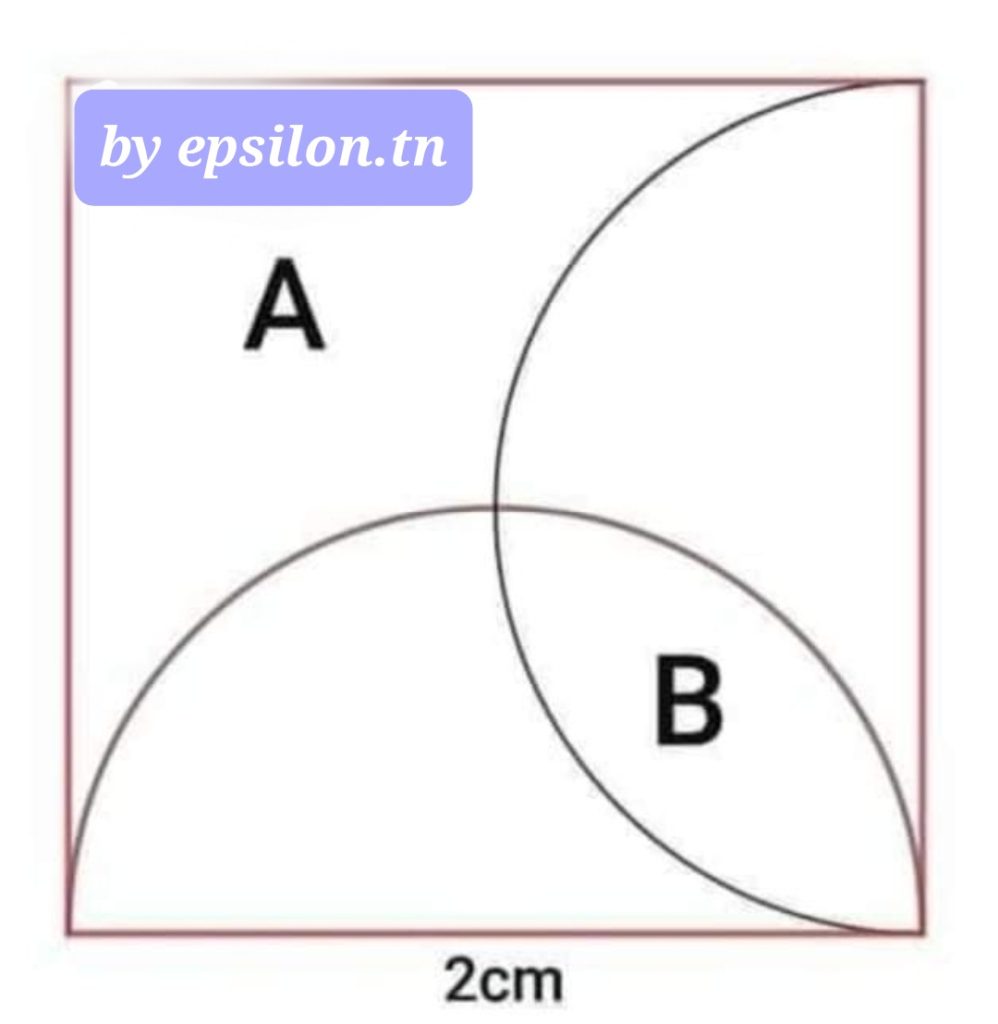
Epsilon 67
Somme des aires des parties A et B.
Que vaut cette somme ?
Epsilon 66
Déterminer l’aire de la partie rouge par deux méthodes différentes.

Epsilon 65
Ce n’est pas un ballon !
Quelle est l’aire de la partie bleue ?

Epsilon 64
Rectangle en partition
Quelle est l’aire du rectangle ?

Epsilon 63
Rectangles et triangles
Quelle est l’aire du rectangle jaune ?

Epsilon 62
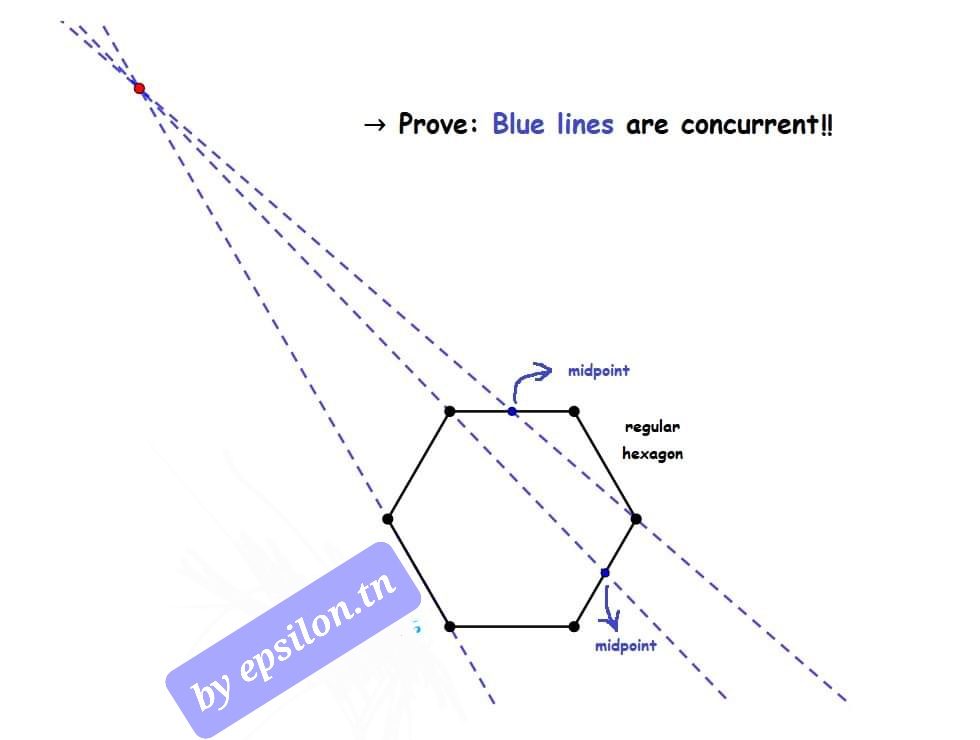
Droites concourantes
Montrer que les droites en pointillé sont concourantes.
Somme de nombres impairs
On commence à partir de 1 et on fait la somme des n nombres impairs successifs jusqu’à 2n-1. Quelle valeur obtient-t-on ?
Epsilon 60
Déterminer la valeur de x.

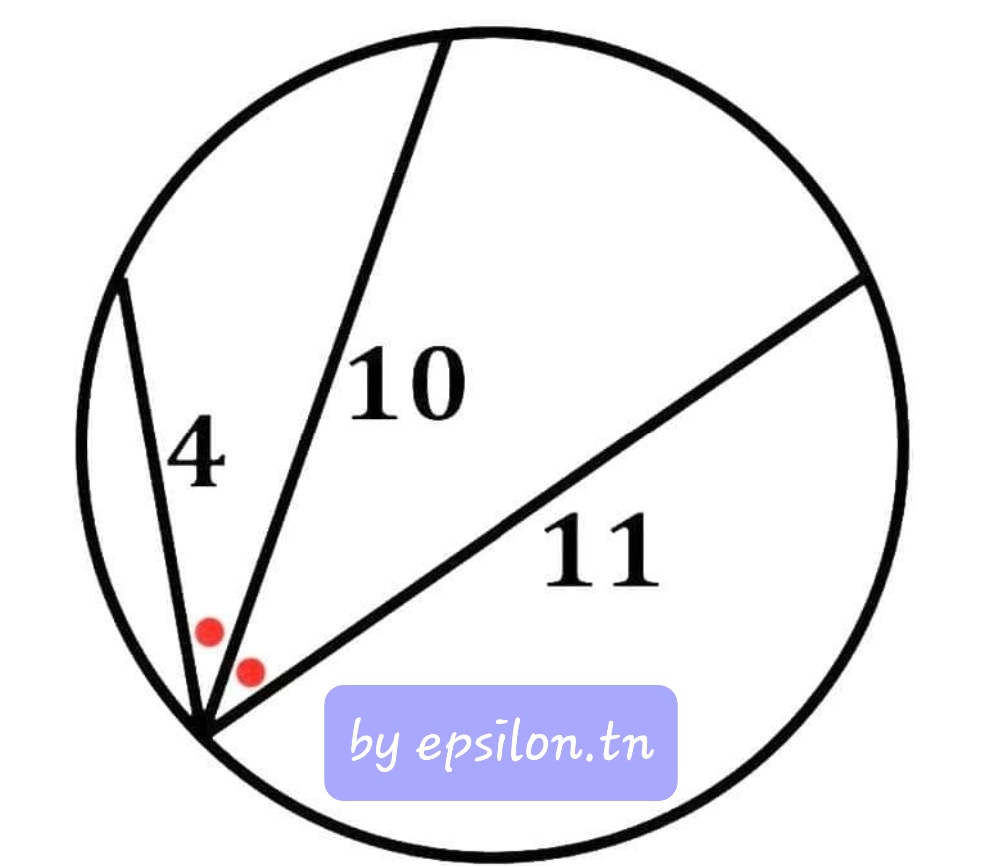
Epsilon 59
Rayon du cercle ?
Les deux angles marqués par un point rouge sont égaux.
Epsilon 58
Quelle est l’aire du trapèze ?

Epsilon 57
Montrer que les 3 points sont alignés

Epsilon 56
Déterminer l’aire du rectangle
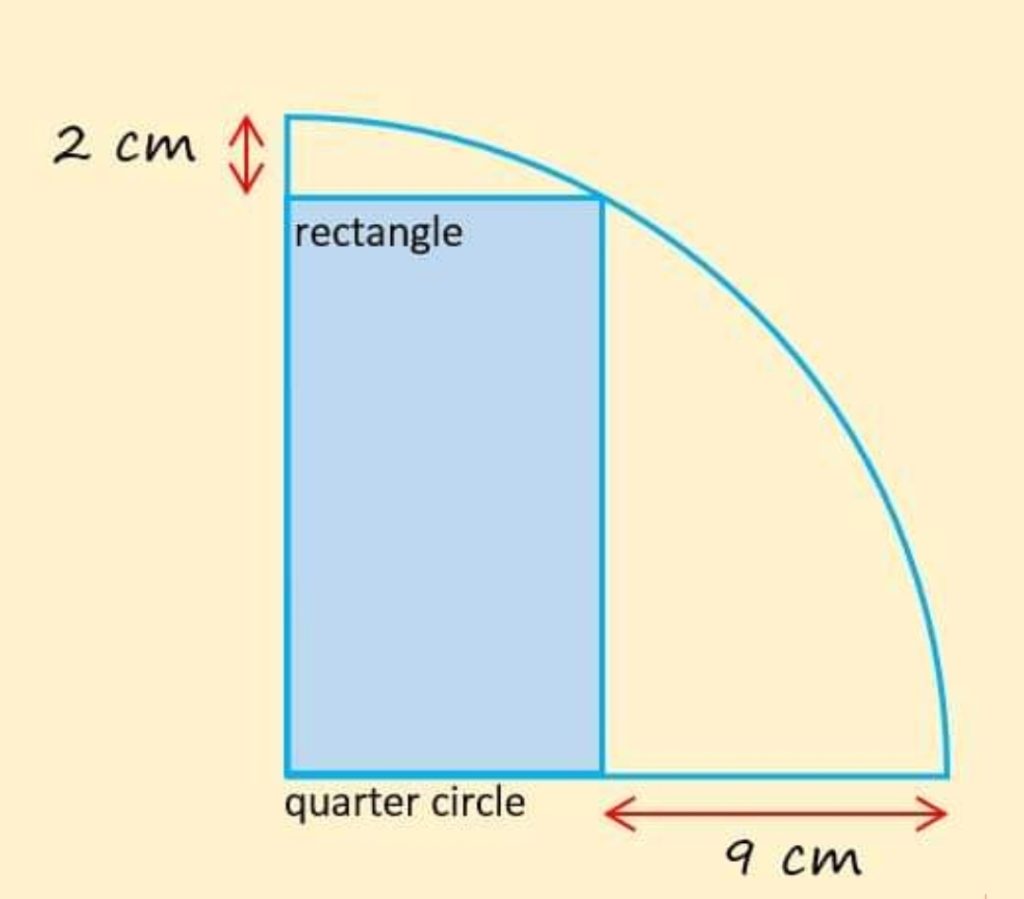
Epsilon 55
Trouver la valeur de x. C’est un nombre entier !

Epsilon 54

Epsilon 53
Aire du triangle bleu ?

Epsilon 52
Pas vraiment facile… à prouver.

Epsilon 51
Trouver l’aire du rectangle

Epsilon 50
Un cercle et deux carrés
Déterminer la somme des aires des deux carrés.
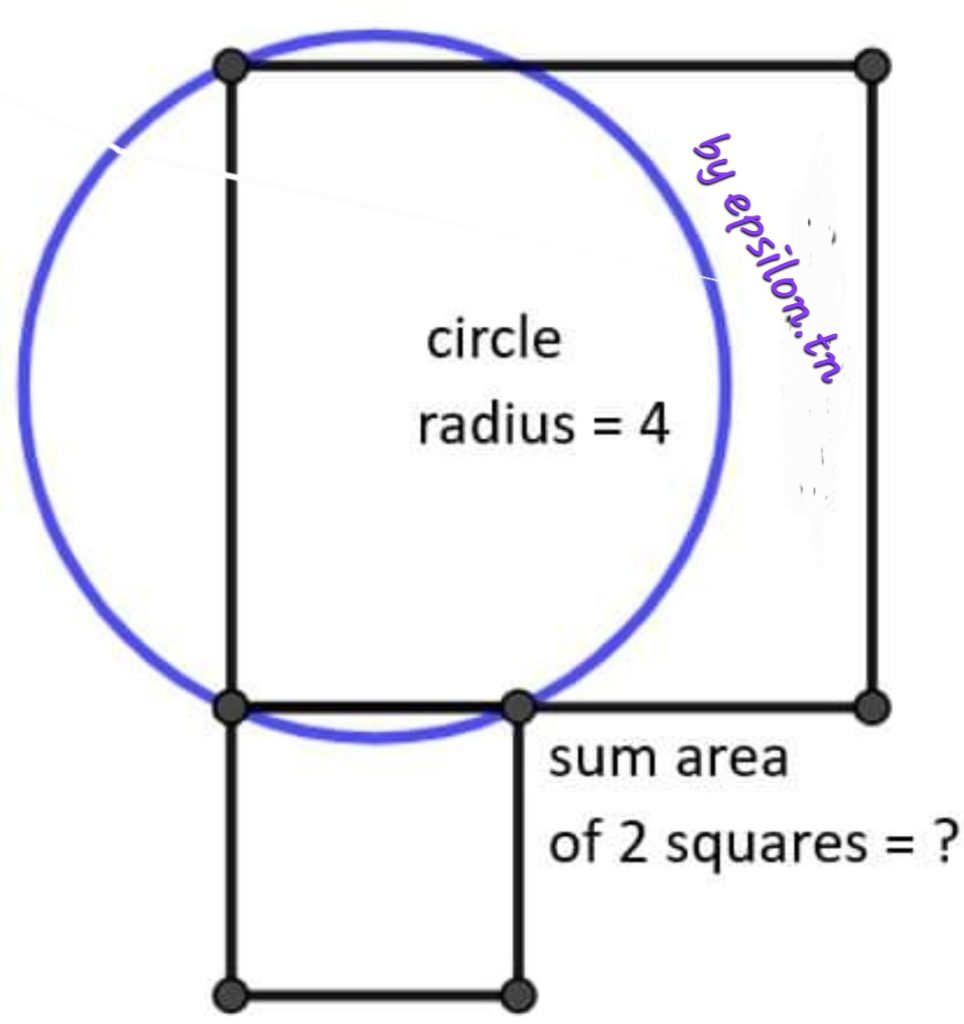
Epsilon 49
Trouver la valeur de a

Epsilon 48
Aire du carré ?

Epsilon 47
Trapèze droit dans un cercle

Epsilon 46
Quel est le pourcentage de la surface bleue du demi-cercle ?
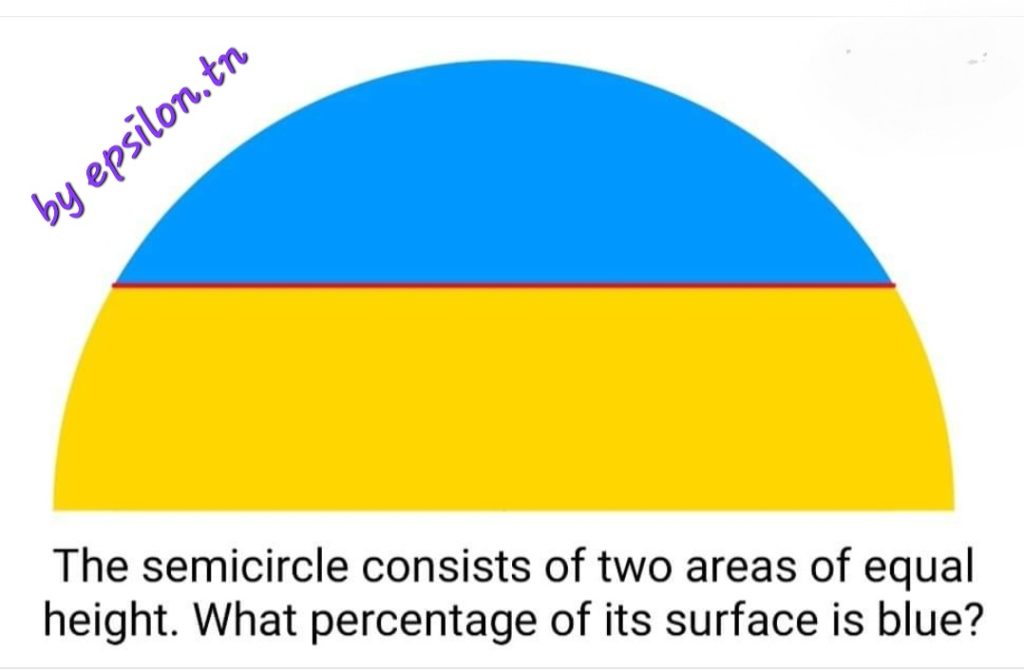
Epsilon 45
Quelle est l’aire du quart de cercle vert ?
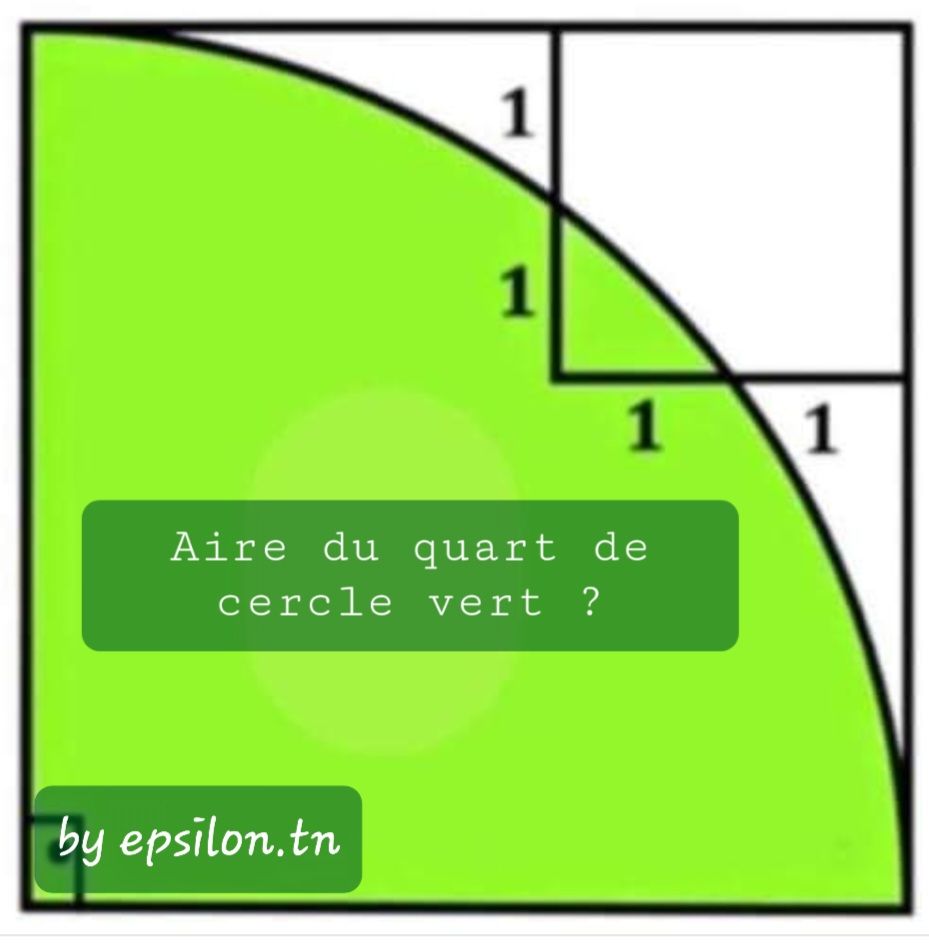
Epsilon 44
Conjecture de Pierre de Fermat
Pierre de Fermat correctly conjectured that there are only two square numbers which are 4 less than a cube.

Preuve ?
Epsilon 43
Trois carrés et un rectangle
Quelle est l’aire de la surface jaune ?

Epsilon 42
Six petits cercles dans un triangle isocèle droit

Epsilon 41
Deux carrés dans un grand carré

Quelle est l’aire du grand carré ?
Epsilon 40
Quel est le carré du rayon du cercle ?

Epsilon 39
Quel est le périmètre du grand rectangle

Epsilon 38
Faisceaux de lumière

Epsilon 37
Aire du carré à partir de celle du triangle mauve.

Epsilon 36
Trouver l’aire du grand carré

Epsilon 35

Epsilon 34
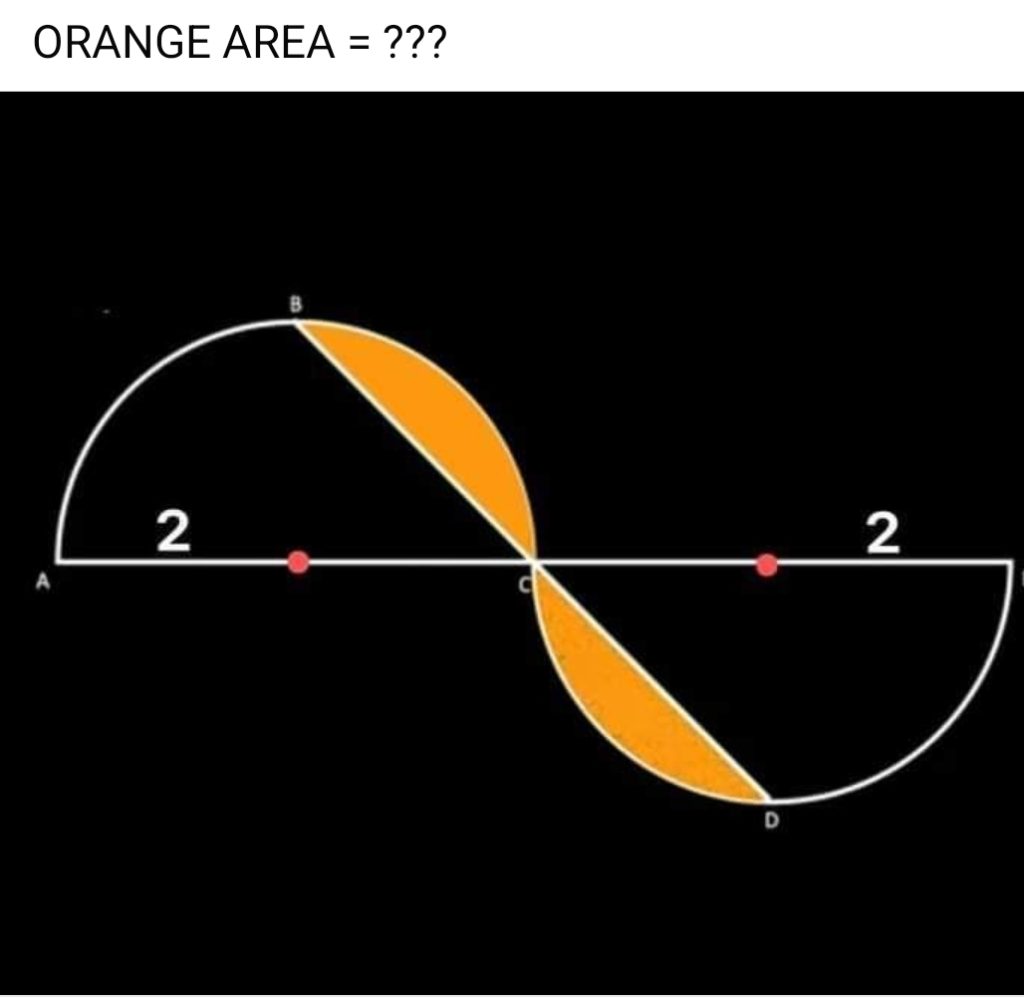
Réponse

Epsilon 33
Quelle est l’aire des dunes bleues.

Epsilon 32
Le triangle est équilatéral. Chaque côté est égal à 1 cm. Déterminer x.

Epsilon 31
Que vaut le rapport zone verte sur zone jaune ?

Epsilon 30
Exercice pour les lycéens

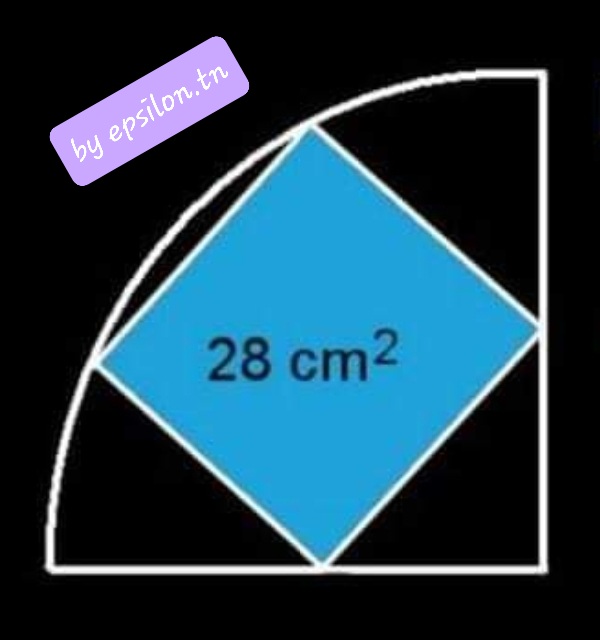
Epsilon 29
Quelle est l’aire du quart de cercle ?
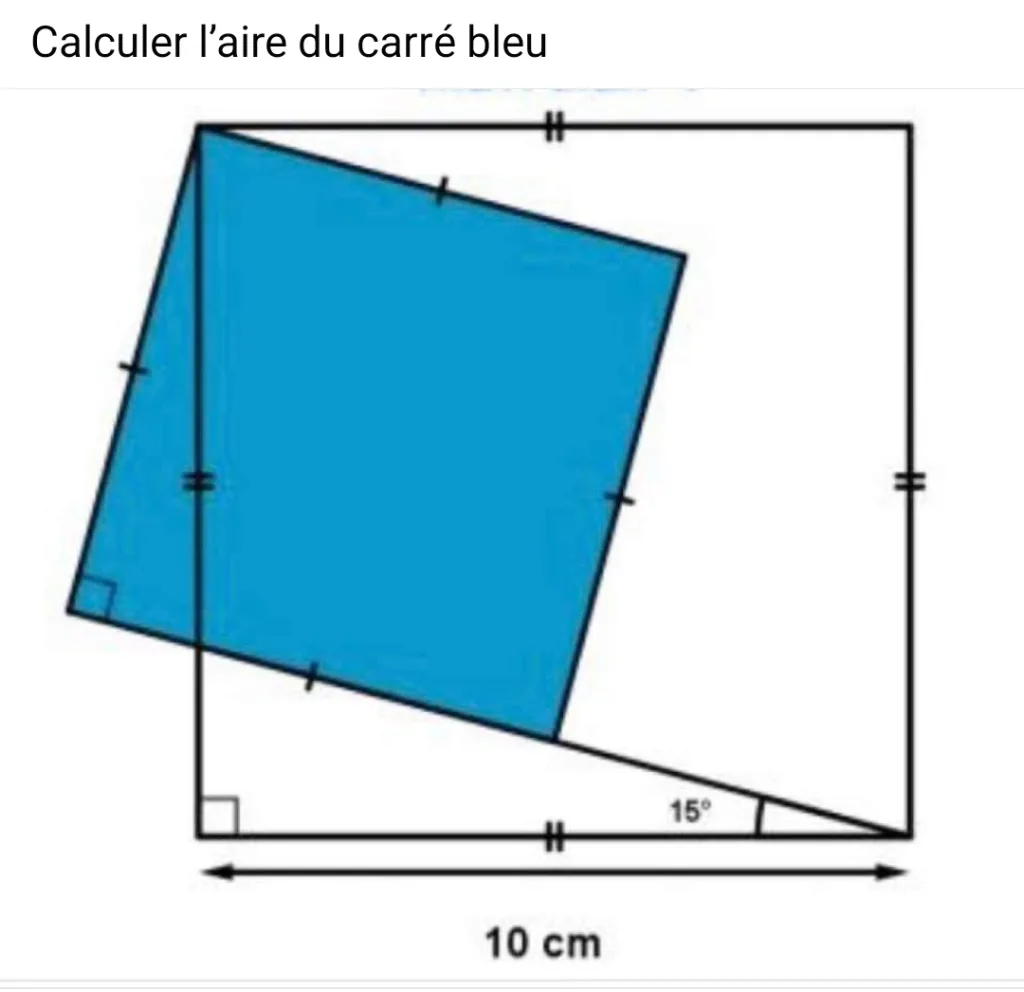
Epsilon 28
Quelle est l’aire du carré bleu ?

Epsilon 27
Quelle est l’aire de la surface bleue
Le diamètre du grand cercle est 12 cm.

Epsilon 26
Deux fois Pythagore !
Déterminer l’aire du rectangle rose.

Epsilon 25
Trouver la valeur de chaque lettre !
Un cryptarithme est une opération mathématique dans laquelle les chiffres ont été remplacés par des lettres, et vérifiant les règles suivantes :
- un chiffre donné sera toujours remplacé par une même lettre;
- une lettre donnée représente toujours le même chiffre;
- aucun nombre ne peut commencer par un zéro
En adoptant cette règle, trouver les chiffres correspondant à chaque lettre pour que les équations suivantes soient vérifiées en même temps:
- RE + MI = FA
- DO + SI = MI
- LA + SI = SOL
Réponse :
O = zéro, S=1, R=2, A=3, D=4, M=5, I=6, E=7, F=8, L=9
Epsilon 24
Deux boules rouges et cinq boules blanches
Une urne contient deux boules rouges et cinq boules blanches. Deux joueurs Ali et Aloulou tirent tour à tour une boule de l’urne sans remise. Ali commence le premier. Quelle est la probabilité que Ali tire le premier une boule rouge.
Epsilon 23
Quelle est l’aire qui est en rouge ?

Epsilon 22
Quelle est l’aire du triangle ABC ?

Epsilon 21
Trouver x

Epsilon 20
Le carré renversé
Epsilon 19
Deux cercles dans un triangle
Calculer le rayon r de chacun des deux petits cercles.

Epsilon 18
L’hôtel avec un nombre infini de chambres
Vous êtes allé à un hôtel qui a un nombre infini de chambres (1 personne max par chambre) mais qui affiche complet. Quelle instruction peut donner le responsable de l’hôtel pour vous libérer une chambre ?
Epsilon 17
Deux cordes dans un quart de cercle

Epsilon 16
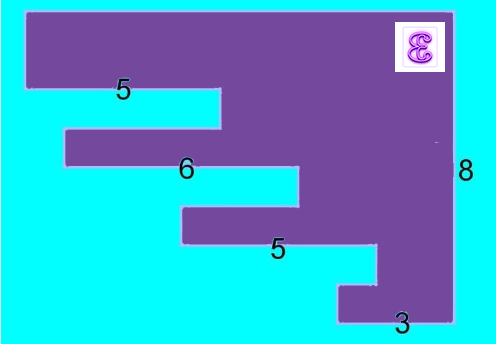
Périmètre d’un polygone à 16 côtés
Quel est le périmètre du polygone mauve ?
Epsilon 15
Les deux petits cercles
Quel est le rayon des deux petits cercles jaunes ?

Epsilon 14
Le cercle au dessus du demi-cercle
Quelle est le rayon du cercle mauve ?

Epsilon 13
Le carré narcissique
Cette énigme est dûe à lemonde.fr

Epsilon 12
Enigme du pêcheur
Un pêcheur part pêcher pendant 3 jours. Le deuxième jour, il pêche au moins un poisson plus que le premier jour. Le troisième jour, il pêche au moins un poisson plus que le second jour mais au moins un poisson moins que la totalité de ce qu’il a pêché pendant les deux premiers jours. Il a pêché au total 12 poissons. Combien a-t-il pêché chaque jour ?
Epsilon 11
Trois points et un heptagone
Considérons un heptagone (c’est à dire un polygone régulier à sept sommets) dont les sommets se trouvent sur un cercle. Quelle est la probabilité pour que 3 de ses sommets choisis au hasard soient dans un même demi-cercle ?

Epsilon 10
Trois points et un pentagone

Considérons un pentagone dont les sommets se trouvent sur un cercle. Quelle est la probabilité pour que trois de ses cinq sommets choisis au hasard soient sur un même demi-cercle
Epsilon 9
Trois points et un polygone

Enigme : Considérons trois points choisis aléatoirement parmi les 2p+1 sommets d’un polygone régulier inscrit sur un cercle. Quelle est la probabilité pour que ces trois points se trouvent dans une moitié du cercle.
Epsilon 8

Probabilité pour que trois points soient sur le même demi-cercle
Trois points sont disposés aléatoirement sur un cercle. Quelle est la probabilité que les trois points soient dans le même demi-cercle ?
Epsilon 7
Un nombre à dix chiffres
Soit un nombre composé de dix chiffres, tous distincts, de telle sorte que le premier chiffre soit divisible par un, le nombre formé des deux premiers chiffres soit divisible par deux … jusqu’au nombre formé par les dix chiffres divisible par dix. Quel est ce nombre ?
Epsilon 6
La suite de Syracuse : On choisit un nombre entier positif, si le nombre est pair, on le divise par 2, si le nombre est impair, on le multiplie par 3 et on lui ajoute 1. On répète le processus avec le nouveau nombre.
La conjecture est que peu importe le nombre avec lequel on commence, on finit toujours par atteindre le nombre 1.
Epsilon 5
[Latexpage]
Montrer que pour tout $n\geq 1$, on a : $ n^{5}-n$ divisible par $30$
Epsilon 4
La conjecture de Goldbach : Cette conjecture affirme que tout nombre pair supérieur à 2 peut être exprimé comme la somme de deux nombres premiers. Par exemple, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5.
Bien que cette conjecture ait été vérifiée pour de très grands nombres, elle n’a toujours pas été prouvée ou réfutée. C’est un problème ouvert. Avis aux amateurs
Epsilon 3

Solution : Cliquer ici
Epsilon 2
J’ai deux fois l’âge que vous aviez quand j’avais l’âge que vous avez. Et quand vous aurez l’âge que j’ai, la somme des nos âges sera égale à 63 ans. Quel est mon âge et quel est votre âge.
Epsilon 1
On veut faire cuire une tarte en 15 min au four. On dispose uniquement de deux sabliers : un de 7 min et l’autre de 11 min. Comment faire ?
Indications:
- Utiliser le fait que 11=7+4
- Bien choisir le moment pour mettre la tarte au four.

