Les mathématiques à travers les siècles
L’histoire des mathématiques remonte aux premières civilisations qu’a connues l’humanité. Ainsi certains papyrus de l’Egypte antique témoignent de problèmes mathématiques que se posaient les égyptiens 18 siècles Av. J.C. en y joignant parfois les solutions. Il est aussi presque certains que les mathématiciens grecs ont puisé dans l’héritage de l’Egypte pour énoncer certains théorèmes dont le plus célèbre, connu de tous les collégiens, est le théorème de Pythagore (vers 450 Av-J.C.). Il semble en fait que Pythagore ait été inspiré par des pratiques de construction d’un angle droit lors de son séjour en Egypte. En effet, les égyptiens utilisaient des cordes avec de gros nœuds à égale distance et les fixaient de manière à former un triangle en prenant un côté avec 3 nœuds, un autre avec 4 nœuds et le troisième avec 5 nœuds (nombre de nœuds avec extrémités incluses pour les trois côtés). Ainsi, l’angle opposé au grand côté de 5 nœuds était nécessairement un angle droit. Pythagore, remarquant que, en fait le carré de la longueur du grand côté était égal à la somme des carrés des longueurs des deux autres côtés, en déduit son célèbre théorème. Toutefois, il semble que la première démonstration écrite de ce résultat est dûe à Euclide ( vers 300 Av-J.C.).

Euclide, voilà un autre nom incontournable de l’histoire des mathématiques. On lui doit un traité sur la géométrie plane « Données« , et une œuvre constituée de 13 livres connue sous le nom « les éléments » qui traite des problèmes de théorie des nombres et de géométrie.
Evidemment, entre l’Antiquité et le Temps actuel, on passe, selon la chronologie et la terminologie communément adoptées par l’Occident, par le Moyen Âge, la Renaissance et les Temps Modernes.
On donne dans la rubrique ε-stars un aperçu sur les prinicipaux mathématiciens de ces époques et, par la même occasion, on rappelle leurs travaux les plus importants. Mais faisons un saut historique pour voir l’une applications les plus récentes et les plus étonnantes des mathématiques qui date de quelques mois seulement, à savoir l’intelligence artificielle générative.
Les maths aujourd’hui … un exemple !
Donnons un exemple que tout le monde connait. L’équation du second degré que voici:
[latexpage]
\[ax^2 + bx + c = 0\]
D’abord, du point de vue forme, cette belle équation est édité sous Latex, le langage d’édition mathématique qui, à la base, est écrit sous la forme d’un code Latex. Pour cette équation, le code est :
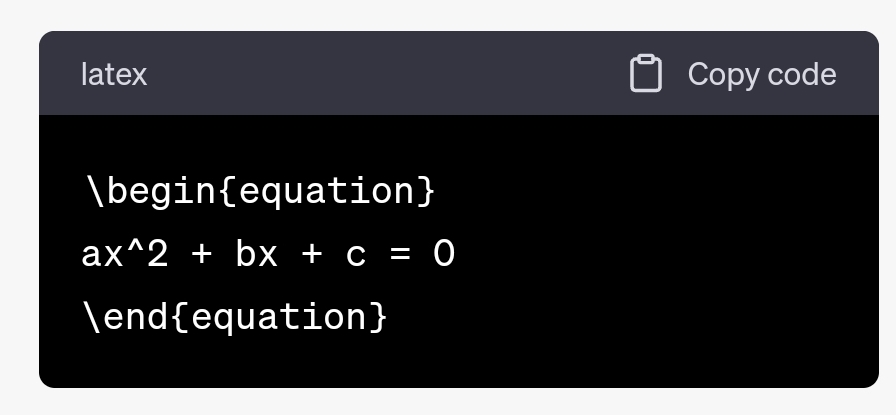
Comme je ne dispose pas d’un éditeur Latex, j’ai généré ce code tout simplement en demandant à ChatGPT de le faire. Et c’est fait en deux clics ! Précurseur de l’intelligence artificielle générative, ChatGPT est en train de faire des émules après avoir fait une petite révolution en fournissant un outil extrèmement performant de création de contenus divers qui n’ont pas beaucoup à envier à la production humaine.
Pour poursuivre avec l’exemple précédent, on peut aussi demander à ChatGPT de fournir la méthode de résolution de cette équation. Voici sa réponse en Latex:
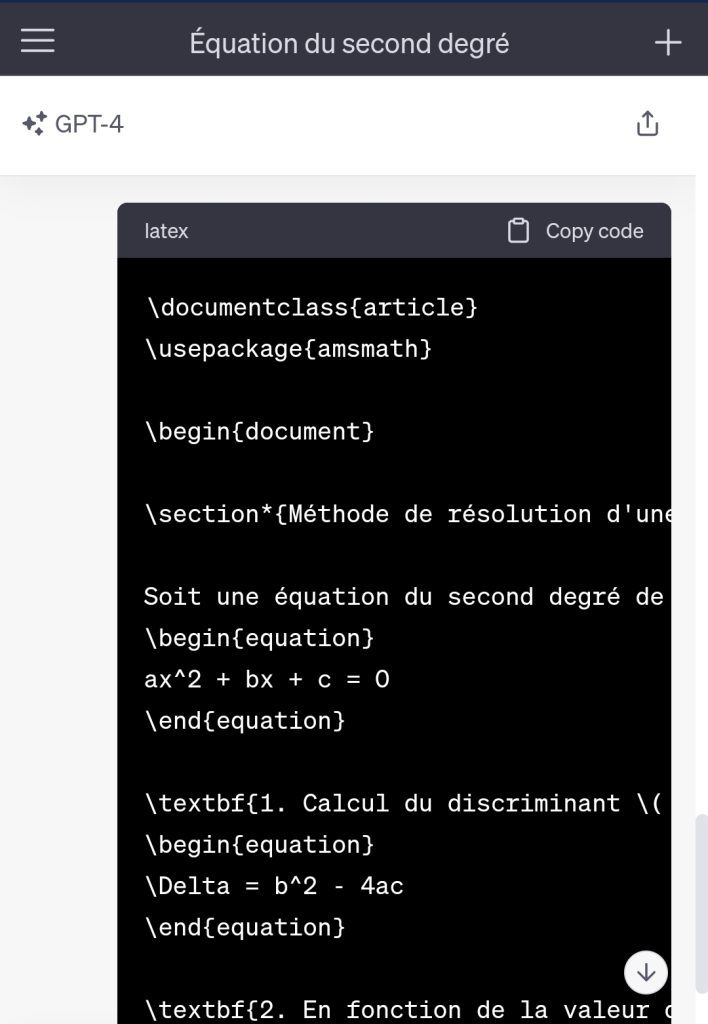
Et, voila ce qu’on obtient après compilation, version lecteur:
[latexpage]
Soit une équation du second degré de la forme:
\begin{equation}
ax^2 + bx + c = 0
\end{equation}
1. Calcul du discriminant \( \Delta \):
\begin{equation}
\Delta = b^2 – 4ac
\end{equation}
2. En fonction de la valeur de \( \Delta \):
Si \( \Delta > 0 \): L’équation a deux solutions réelles distinctes:
\begin{align}
x_1 &= \frac{-b – \sqrt{\Delta}}{2a} \\
x_2 &= \frac{-b + \sqrt{\Delta}}{2a}
\end{align}
Si \( \Delta = 0 \): L’équation a une unique solution réelle:
\begin{equation}
x = \frac{-b}{2a}
\end{equation}
Si \( \Delta < 0 \): L’équation n’a pas de solutions réelles, mais deux solutions complexes conjuguées:
\begin{align}
x_1 &= \frac{-b – i\sqrt{-\Delta}}{2a} \\
x_2 &= \frac{-b + i\sqrt{-\Delta}}{2a}
\end{align}
Les maths aujourd’hui … beaucoup de maths derrière ChatGPT !
L’exemple exposé plus haut, encore inimaginale il ya quelques mois, ne donne qu’un cas simple de tout ce qui peut être fait avec l’Intelligence artificielle (IA). Mais ce qu’il faut savoir, c’est qu’en arrière plan de l’IA, il y a beaucoup de mathématique, essentiellement dans le champs de la statistique et de l’analyse de données massives. Evidemment, l’informatique couplée à la puissance de calcul qui permet de traiter des quantités « infinies » de données assure le soutien logistique aux algorithme de l’IA. C’est dire que les mathématiques sont au coeur de la nouvelle révolution technologique induite par les avancées de l’IA. Toujours et encore les maths !




